前言
傅里叶变换是许多理工科都会用到的一种线性积分变换。传统的卷积神经网络(CNN)无法在非欧数据上运算,为了能够在图等非欧数据上进行卷积运算,研究人员提出在图上进行傅里叶变换,进而发展出图卷积网络(GCN)。
本文将聚焦于傅里叶级数和傅里叶变换的数学推导,完全从数学的角度展开。若想了解傅里叶分析的基本概念,可以参考这篇文章。这个视频对本文的写作具有启发性意义,本文的一些地方参考了视频。
三角函数
三角函数的和差公式
为了真正从零开始推导,首先需要掌握三角函数和差公式。假设平面上有两个单位向量,与x轴的正向夹角分别为
在欧几里得空间中,内积可以直观地定义为两个向量的模长乘它们之间的余弦夹角,即
此时我们得到了第一个三角函数和差公式
即
这里用到了
公式(2),(4),(5),(6)就是三角函数最基本的和差公式,是后续推导的基础。
三角函数的正交性
先来看一个三角函数的集合:{ 0,1,sinx,cosx,sin2x,cos2x,…,sinmx,cosmx,…},这实际上是由sinnx和cosnx组成的集合,其中n为自然数。
正交
这里引用维基百科中正交的概念——“正交是线性代数的概念,是垂直这一直观概念的推广。若内积空间中两向量的内积为0,则称它们是正交的。”也就是说,当两个向量正交时:
其中
当
当式(3)为0时,两个向量正交。
对于任意两个三角函数在区间
同样可以计算
当
注意,这里其实用到了一个小trick,即
同样可以计算当
傅里叶级数
讲了那么多铺垫,终于进入到第一个主题,傅里叶级数。首先,我们来看一下傅里叶级数的定义,这里同样引用维基百科的定义——“傅里叶级数是把类似波的函数表示成简单正弦波的方式。更正式地说,对于满足狄利克雷定理的周期函数,其傅里叶级数是由一组简单振荡函数的加权和表示的方法。”现在我们知道了傅里叶级数是什么东西,它无非就是一组具有周期性的简单振荡函数的加权和,那么我们就可以开始计算了。我们先看一个最简单的正弦函数,
现在,我们根据傅里叶级数的定义,假设(16)是满足狄利克雷定理的周期函数,那么它的傅里叶级数就是(16)的加权和,即
由于
这一步实际上就是把加和项0拿出来单独计算,于是加和从1开始,
这一步实际上也用到了三角函数正交性的trick,因为
得到
(21)中等式右边第一项由于
因此
同理可得
此时我们算得了
可以看到,
当
上面的等式是我们为了便于计算而假设了周期是
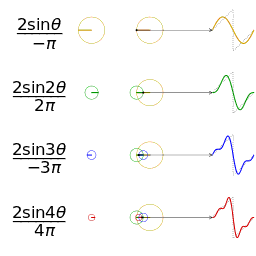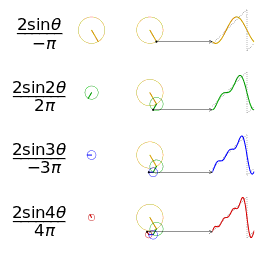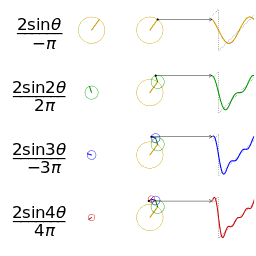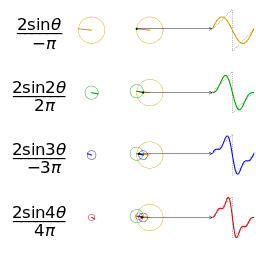
图1 一个相同幅度和频率的锯齿波的近似
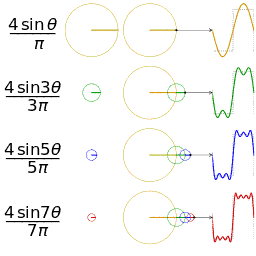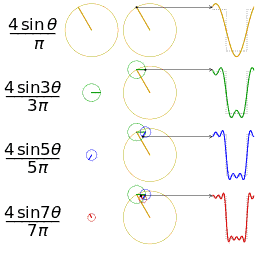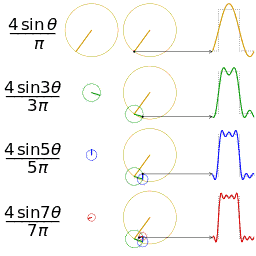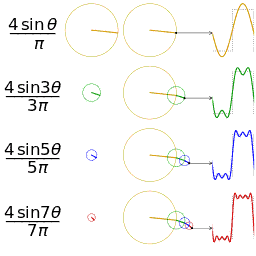
图2 另一个分别采用傅里叶级数的前 1, 2, 3, 4 项近似方波的可视化。
这个网站可以看到傅里叶级数交互式的动画。
欧拉公式
在介绍傅里叶变换前,需要先介绍宇宙最美公式——欧拉公式。本节只证明而不介绍欧拉公式,想要了解欧拉公式,可以参考李永乐老师的视频。我们假设
因此
将(29)中的
利用[(30)-(29)]/2和[(30)+(29)]/2分别可以得到
傅里叶级数的复数形式
将公式(31),(32)带入公式(26)中,有
这一步比较复杂,需要具体解释一下。第一个等号实际上就是把公式(31),(32)带入公式(26)中,等二个等号用到了乘法结合律,第三个等号是关键,这里把第一项的
现在我们将(27)带入(34)中,当
当n为正整数时,
当n为负整数时,
算到这里时,我们发现当
现在,
其中
傅里叶变换
上文已经阐述了当周期是
.gif)
图3 傅里叶变换将函数的时域(红色)与频域(蓝色)相关联。频谱中的不同成分频率在频域中以峰值形式表示。
图3很好的展示了通过傅里叶变换将正弦波组成一个类方波的过程,现在依次解释图3中发生了什么。
.gif_20220528_203521.118.jpg) (a)
(a) .gif_20220528_203548.049.jpg) (b)
(b) .gif_20220528_203525.421.jpg) (c)
(c) .gif_20220528_203559.910.jpg) (d)
(d) .gif_20220528_203608.822.jpg) (e)
(e) 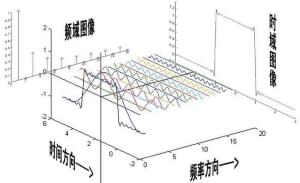 (f)
(f)上文已经推导出当周期为T时,
其中
当周期趋向于无穷大时,
其中
称为傅里叶变换,
称为傅里叶逆变换。到此为止,我们已经推导完傅里叶变换和傅里叶逆变换,如果你动手跟着文章一路推导下来,那么你应该理解了本篇文章的内容,接下来你就可以应用它啦。
- Post title:从零开始推导傅里叶变换
- Post author:jamiehz
- Create time:2022-05-28 21:41:01
- Post link:https:jamiehz.github.io/2022/05/28/从零开始推导傅里叶变换/
- Copyright Notice:All articles in this blog are licensed under BY-NC-SA unless stating additionally.